-
 Graham John
3326 new methods have been added to the CCCBR Methods Library this week:
Graham John
3326 new methods have been added to the CCCBR Methods Library this week:
Minor: Sudeley Manor Bob
Major: Daisy Delight, Metro Alliance, Tarcutta Surprise, Ugrosaurus Surprise, Widecombe Fair Surprise
methods.cccbr.org.uk -
 PeterScott
76These MethodLibraryUpdates seem so lonely :-)
PeterScott
76These MethodLibraryUpdates seem so lonely :-)
It's a brilliant resource to have the methoids on Complib, just a click away from a diagram, and ready-to-ring.
Sadly, locally, we don't have the resources to select one of the new methods every week as a challenge for practice night. It would be fun to think that some bands might take this on, and give a user-assessment of one of the new methods each week. Maybe the RW could publish What's Hot On Complib to accompany Bellboard's hotnesses.
Best I could do was click on Sudeley Manor Bob which Complib helpfully identifies as the two hundred and forty-first TrivialVariation of Double Oxford Bob Minor.
It's just too tempting to click some of the others in the list, for example Bob Bob Minor is an assymetric three-blows method; then, less trivially, Double Danbury Bob Minor
The place notation shows it's rotationally symmetric (14 to 36, 1236 to 1456), but not in the traditional sense, Double. First rung here. Complib disagrees with my symmetry analysis. Hmmmmm ...-14-1236-1256-36-1456-1256
And only 238 more to go ... -
 Graham John
332The place notation shows it's rotationally symmetric (14 to 36, 1236 to 1456), but not in the traditional sense, Double. First rung here. Complib disagrees with my symmetry analysis. — PeterScott
Graham John
332The place notation shows it's rotationally symmetric (14 to 36, 1236 to 1456), but not in the traditional sense, Double. First rung here. Complib disagrees with my symmetry analysis. — PeterScott
Symmetry is dependent upon the axis of rotation chosen for the three terms: Palindromic, Double & Rotational. Complib is consistent with the Framework for Method Ringing and former CC Decisions on this definition. The use of the prefix Double in method titles is equally consistent. Column 1 below is Double Danbury Bob Minor and columns 2, 3 and 4 are column 1 rotated using three different axes. The column with the same blue line as column 1 tells you the symmetry. In this case Double but not Palindromic or Rotational.
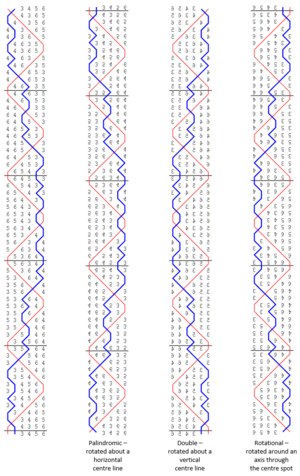
-
 PeterScott
76Yes, I enjoyed the diagrams, thanks.
PeterScott
76Yes, I enjoyed the diagrams, thanks.
I like this 1998 definition of a Double Method, with my emphases:
from the CCCBR publication The Tower Handbook 1998 ISBN 0 900271 44 2 Complied by .What is a double method? It has a special sort of symmetry. All regular methods are symmetrical - if you look at the 'blue line' you will find an axis of symmetry from which point the progress of the line is a mirror image of what has gone before. ...A double method has two axes of symmetry, so that the work on the front when the treble is at the back is the mirror image of the work at the back when the treble is at the front. In fact the whole of the work over the treble is a mirror image of the work under the treble. … Many double methods have double in their name - Double Bob, Double Oxford, Double Norwich - but some, most notably Bristol and Superlative Surprise, do not….
The Council, in a new Decision at its 2004 meeting codified a Double Method for the first time, having relied on customary ringers’ terminology before this:
.(E).A.7 - A method has palindromic symmetry if it is the same method when rung backwards, that is when the order of the changes is inverted. A method has double symmetry if it is the same method when reversed, that is when the places within each change are inverted. A method has rotational symmetry if it is the same method when reversed and rung backwards.
This definition survived in the Decisions until superseded by the Framework in 2018-2019, which phrased the rules as:
4.B.1. Palindromic Symmetry: A Method has Palindromic Symmetry if the same Changes result (after Rotation if needed) when read backwards, that is, when the order of the Changes is inverted.4.B.2. Double Symmetry: A Method has Double Symmetry if the same Changes result (after Rotation if needed) when reversed, that is, when the Places within each Change are inverted.4.B.3. Rotational Symmetry: A Method has Rotational Symmetry if the same Changes result (after Rotation if needed) when reversed and read backwards.
Double Methods, as defined in 1998, have a mathematical elegance, are artistically pleasing, help practical ringing and are an essential part of Ringing Heritage. (As an aside, the natural meaning of Double is its two-ness, and this is preserved. Also see here:Reveal}Other ringers’ terminology respects the natural meaning of Double. I can ring handbells double-handed and double dodges in Doubles with all double-changes and not be ringing a Double method. (Stedman Doubles)
To redefine them, and to do that - in my assessment - accidentally, is a real shame and should be undone.
Turning to 2004, there had been no earlier Decision which tried to codify a Double Method. All ringers reading that new version would, as I did at the time, think it was good-enough. It would have been better to have a proper definition of “rung backwards” to remove any ambiguity. (Brief aside here:Reveal) The Decisions were never designed-as-a-whole and there were all manner of quirks and ambiguities in the wording and it was just-in-passing to notice this one, and forgive it ...The term “rung backwards” doesn’t have complete precision: surely starting Plain Bob Minor backwards, with the change 12 will then have all the leading at backstroke-then-handstroke and not feel like Plain Bob Minor at all. Similarly “Go Backward Hunt” is designed exactly to achieve wrong-leading.
The new Decision then goes on to say that if you now reverse the method, and it is still the same method, then it is a Double Method. That too was wholly in line with the customary definition, while talking of the overwhelmingly predominant (then as now, see current example here:Reveal) symmetric methods, it is saying the same thing as the 1998 Tower Handbook definition, and there was no particular reason to comment. …For an example of this overwhelming predominance, consider the 2023 Ringers’ Diary, Start from the 1stJanuary and work backwards through the method pages, counting the bluelines and how many are symmetric. For the impatient, click here:Reveal- Maximus: 18 bluelines, all symmetric.
- Cinques: no bluelines
- Royal: 17 bluelines, all symmetric.
- Caters: 7 bluelines, all symmetric.
- Major: 61 bluelines, all symmetric.
- Triples: 19 bluelines, all symmetric.
- Minor: 45 bluelines, all symmetric.
- Doubles: 22 bluelines, all symmetric.
- Minimus: 20 bluelines, all symmetric.
- Singles: 5 bluelines, 4 symmetric, and Shipping Forecast Singles on p18
(errors and omissions excepted)
But to be pedantic, that full stop between the sentences might have been better as a semicolon. And the last sentence is only worth saying about not-palindromic methods.
Then to 2018/2019: I wasn’t party to all the discussions during Framework development: it seems to me that the 2004 definition was carried-forward without analysing its probably-unintended ambiguity. Using the Framework definition has a not-palindromic method as “Double” with only (in the 1998-terminology) one axis of symmetry.
Sadly I could go on ... -
 Graham John
332You have a point, Peter, if you mean that Double should mean rotation about two points of symmetry.
Graham John
332You have a point, Peter, if you mean that Double should mean rotation about two points of symmetry.
I don't know the reasoning behind the 2004 definitions, but it could be trying to fit the existing methods that had Double in their name. In other words, they were following precedent. Looking at the 34 methods that are Double, but not Palindromic, the earliest is Double Eastern Bob Major, which was first pealed in 1752! The others with Double in their name rung before 2004 are: Double Eastern Bob Royal (1973), Double Ascension Cyclic Bob Maximus (2002), Double Cambridge Cyclic Bob Major (2002) and Double Resurrection Cyclic Bob Royal (2002). Perhaps it is the flurry in 2002 that triggered the Methods Committee's definition.
Interestingly there is only one rung method currently that has Double and Rotational symmetry that is not Palindromic: Te Deum Treble Place Singles.
Welcome to your Ringing Forums!
If you would like to join in the conversation, please register for an account.
You will only be able to post and/or comment once you have confirmed your email address and been approved by an Admin.
Categories
- BELL INSTALLATION & RESTORATION PROJECTS
- CALL CHANGES
- CCCBR Consultation
- EDUCATION AND TRAINING
- GENERAL
- MEMBERSHIP SOFTWARE
- MEMBERMOJO
- METHOD RINGING
- METHODS
- COMPOSITION
- CONDUCTING
- HANDBELL RINGING
- PUBLIC RELATIONS
- RECRUITMENT & RETENTION
- Ringing 2030
- RINGING SIMULATORS AND SOFTWARE
- RUNNING A TOWER
- TOWER MAINTENANCE
More Discussions
- Contact Us
- RingingForums Policy
- Terms of Service
- Useful Hints and Tips
- Sign In
- © 2026 Ringing Forums


